חזקות של מטריצות ופולינומים של מטריצות
תהי A מטריצה ריבועית . החזקות של A מוגדרות כלהלן:
|
A0=I , A2 = AA , A3 = A2A ... An+1 = An A |
נגדיר גם פולינומים של מטריצה A באופן הבא :
לכל פולינום f(x) = a0 + a1x + a2x2 + ... anxn
כאשר ai הם סקלרים f(A) מוגדרת כמטריצה:
f(A) מתקבלת מ- f(x) ע"י הצבת המטריצה A במקום המשתנה x והצבת המטריצה הסקלרית a0I במקום הסקלר a0.
במקרה שבו f(A) היא מטריצת האפס,
המטריצה A נקראת אפס או שורש של הפולינום f(x) .
כהרגלנו נסביר את הנושא באמצעות דוגמא:
דוגמאות
תהי 
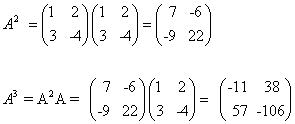
אם f(x) = 2x2 - 3x + 5 אזי:
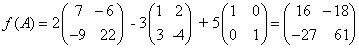
אם g(x) = x2 + 3x - 10 אזי:
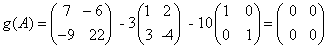
תכונות של פולינומים של מטריצות:
יהיו f(x) ו- g(x) פולינומים ותהי A מטריצה n ריבועית אזי:
א) (f+g)(A) = f(A) + g(A)
ב) (fg)(A) = f(A)g(a)
ג) f(A)g(A) = g(A)f(A)
נסביר את התכנות:
שתי התכונות הראשונות טוענות כי אם אנו מחברים (כופלים) את הפולינומים f(x) ו- g(x) ואז מציבים בסכום (במכפלה) את המטריצה A , אנו משיגים אותה תוצאה כאילו חישבנו קודם את f(x) ו- g(x) ב- A ואז חיברנו (כפלנו) את המטריצות f(A)g(A)
התכונה השלישית טוענת כי כל שני פולינומים ב-A מתחלפים.
גולשים מקוונים: 5