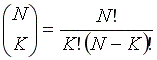|
פונקצית הסתברות של המשנה המקרי X הוא רשימת הערכים שמקבל משתנה מקרי בדיד X כולל ההסתברויות לכל ערך.
אחת הדרכים הנוחות ביותר להציג את פונקצית ההסתברות של משתנה מקרי בדיד היא באמצעות טבלה:
|
|
|
|
שים לב לתכונה חשובה:
בכל משתנה מקרי בדיד סכום ההסתברויות של כל הערכים בטווח של במשתנה המקרי הוא 1, וכן למשל עבור המשתנה המקרי X בטבלה הנ"ל מתקיים:
|
|
עבור משתנים רציפים אנו נדבר על פונקצית צפיפות כאשר השטח הכולל מתחת לעקומת פונקצית צפיפות הוא ההסתברות שהמשתנה יקבל ערך קטן או שווה ל- x כלשהו.
השטח הכולל מתחת לעקומת פונקצית צפיפות חייב להיות 1.
פונקצית צפיפות של המשתנה המקרי הרציף X , היא פונקציה אי שלילית והשטח הכולל בין עקומת הפונקציה וציר Xשווה ל-1.
השטח מתחת לעקומה בין כל שני ערכים X=a ו- , שווה להסתברות : (P( a < X < b X=b
|
|
קיימות בסטטיסטיקה מספר התפלגויות תיאורטיות חשובות בעלות פונקציות מתמטיות מוגדרות , אשר באמצעותן ניתן לחשב הסתברויות של מאורעות שונים.
התפלגויות אלו מתבססות על מספר הנחות , אשר עקב פשטותן הן מטיבות לתאר את התפלגויותיהן של תופעות אקראיות רבות.
נוהגים לחלק התפלגויות אלו לשתי קבוצות , בהתאם לאופי המשתנה המקרי בו מטפלת ההתפלגות:
א. קבוצת ההתפלגויות הבדידות , הכוללת בין השאר את ההתפלגות הבינומית, ההתפלגות הגיאומטרית, ההתפלגות הפואסונית וההתפלגות המולטינומית.
ב. קבוצת ההתפלגויות הרציפות , הכוללת בין השאר את ההתפלגות הנורמלית , ההתפלגות האחידה וההתפלגות האקספוננצילית. להלן תוצגנה פונקציות ההסתברות התוחלות (ממוצעים) של התפלגויות אלו .
בהמשך נזדקק לנוסחת הצירופים הבאה: |
|
 |
||
יום שבת 26 באפריל 2025
|
|
|
|||||||||||||||||||||||||||||