מדרון משופע

אחד המקרים השכיחים בהם יש צורך להשתמש בפירוק וקטורי הכח לרכיבים הוא המקרה של מדרון משופע.

נראה דוגמה:

מזחלת עם מסה m נמצאת על מישור משופע בזווית 30 מעלות. בציור שלפניכם מצויירים וקטורי הכח שלמדנו עליהם- כח הכבידה כלפי מטה, הכח הנורמלי הפועל על המזחלת בכיוון מאונך למדרון, וכח החיכוך, הפועל בכיוון משיק למדרון, כך שהוא שואף לעצור את המזחלת מלהידרדר למטה.

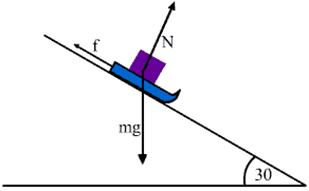
אנו יודעים שני דברים ברורים על המערכת:

1. אין שום תנועה בכיוון האנכי למדרון.
2. כל התנועה היא רק בכיוון המאונך למדרון.

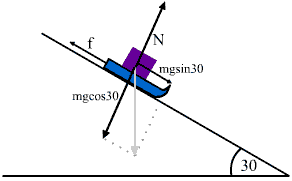
כיוון שהבעיה מתוארת יפה ע"י הכיוונים הנ"ל, נבטא את כח הכבידה בעזרת שני רכיבים, האחד בכיוון משיק למישור והשני בכיוון מאונך למישור.

הפירוק מתבצע על פי מה שלמדנו בפרק ההקדמה על וקטורים.

חשוב לזכור! - לאחר שפירקנו את וקטור כח הכבידה לשני רכיבים, יש להתעלם ממנו. שני רכיביו מחליפים אותו לכל דבר ועניין. זו הסיבה שבציור הבא הוא מופיע בצבע קלוש יותר מהווקטורים האחרים.

כיצד בפועל נתמודד עם מישור משופע עם חיכוך? בזאת עוסק הסרטון הבא הסרטון הבא:

לסיום פרק זה ניתן כמה דגשים לפתרון בעיות בהם מעורבים כמה גופים:

• ראשית יש לכתוב את הכוחות המוכרים לנו הפועלים על כל גוף (נורמלי, חיכוך, כבידה וכו'). אם כח מסויים אינו ידוע, יש לציינו כנעלם. כך יש לעשות עם כל גוף בנפרד. חשוב לזכור שחוטים מושכים את מי שמחזיק בקצותיהם בכוחות שווים והפוכים בכיווניהם.
• עבור כל גוף, יש להחליט מהי מערכת הצירים הטובה ביותר (כמו שראינו במישור משופע למשל), ויש לפרק את הכוחות על מערכת הצירים המתאימה.
• יש לכתוב את כל המשוואות הידועות. הנעלמים יימצאו מתוך שיקולים של תיאום התנועה בין הגופים. למשל- אם ידוע שתאוצתם של שני גופים שווה, או שמהירותם שווה. או אם ישנו יחס בין תנועתו של גוף אחד לזו של חברו.

נדגים בעיית כוחות עם כמה גופים