תנועה מעגלית

 

כבר ראינו כשלמדנו על תאוצה, שכאשר התאוצה פועלת בכיוון מאונך למהירות, היא משנה רק את כיוון המהירות ולא את גודלה.

כמו כן הראנו שכאשר גוף נע במעגל במהירות שגודלה קבוע, הרי שאנו יודעים על תאוצתו שני דברים:

1. כיוון התאוצה נשמר באופן קבוע במאונך לכיוון המהירות.
2. גודל התאוצה נתון ע"י הנוסחה: .

 

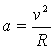מדוע נשמרת התאוצה מאונכת למהירות? מה קובע את גודל התאוצה ומה הסיבה לה? כשלמדנו קינמטיקה עוד לא היינו יכולים לענות על שאלות אלה. עכשיו יש בידינו להשלים את התמונה.

 

כיוון שעכשיו ידוע לנו החוק השני של ניוטון, F=ma, אנחנו יכולים לקבל לא רק את התאוצה בה נע גוף הסובב במעגל במהירות קבועה (בגודלה), אלא גם את הכח הגורם לתנועה זו:

 

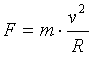
כלומר, אם גוף שמסתו m סובב במעגל שרדיוסו R במהירות v, ברור שמשהו מפעיל עליו כח F המאונך לכיוון תנועתו, ושגודלו נתון על פי הנוסחה הנ"ל.

 

נראה דוגמה:

כביש מוגבה בזווית a כך שניתן ליסוע בו במהירות מבלי להחליק גם אם הכביש חלק לחלוטין. מהי המהירות המקסימלית שניתן ליסוע בה בכביש?

 

נשרטט את הכוחות שאנו מכירים שקיימים במערכת- כח הכבידה כלפי מטה, והכח הנורמלי בכיוון מאונך לפני הכביש:

 

  

 

 

 

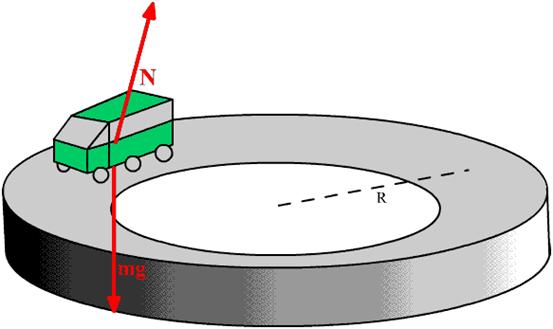
הצעד הבא הוא לראות מהו הכח הגורם לסיבוב של הרכב במעגל. כדי לבודד כח זה נפרק את כל הכוחות לרכיבים שהם או בכיוון הרדיוס, או מאונכים לרדיוס:

 

 

 

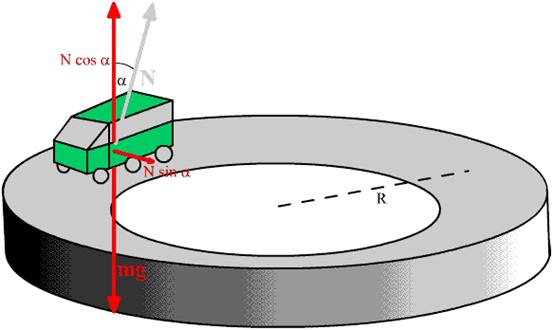
בציר מעלה מטה אין תזוזה (אם היתה כזו, משמעות הדבר היתה שהמכונית מחליקה מהכביש) ולכן ניתן לכתוב:

 

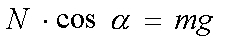
הכח היחיד הפועל בכיוון אנך למהירות (כיוון הרדיוס) הוא הרכיב 

N×sin a של הכח הנורמלי. ולכן ניתן לדעת אותו מתוך הנוסחה לכח מרכזי מסובב ולכתוב:

 

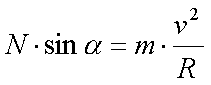
הגענו לשתי משוואות בשני נעלמים- N ו-a. נחלק את המשוואה השניה בראשונה ונקבל:

 

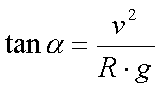
כלומר, ככל שהמהירות גדולה יותר והרדיוס קטן יותר, יש צורך בזווית שהטנגנס שלה גדול יותר, כלומר, זווית הגבהה גדולה יותר.

 

נזכור כלל חשוב בפתרון בעיות מסוג זה:

הכח 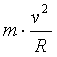 , אינו כח במלוא מובן המילה כמו כח הכבידה, הכח הנורמלי או כח החיכוך. לכן, יש לצייר בתחילה רק את הכוחות המוכרים הנ"ל. לאחר שאנו יודעים מהם הכוחות המכוונים במקביל לרדיוס הסיבוב (כוחות מאונכים למהירות, כלומר, כוחות מסובבים), ומתוך ידיעתנו את מהירות הסיבוב ואת רדיוסו, נוכל להשוות אותם לביטוי   .

 

 

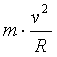כאשר אנו נוסעים ברכב, והרכב פונה, אנו מרגישים כח הדוחף אותנו בכיוון מנוגד לכיוון פניית הרכב. הסברנו כבר מדוע על גופים הסובבים במעגל פועל כח כלפי מרכז המעגל. עם זאת, הדוגמא הנ"ל מעלה שאלה- מאין בא הכח שמרגיש הנוסע ברכב? הרי הוא מכוון הפוך ממרכז הסיבוב!

התשובה טמונה בעובדה שהרכב ונוסעיו, אינם מרכיבים גוף הומוגני. ננסה להסביר-

נתבונן בדוגמה של הרכב הפונה פניה חדה ומהירה- הרכב משנה מכיוון מהירותו משום שהכביש מפעיל עליו כח לכיוון מרכז הסיבוב. כדי לגרום לנוסעים להסתובב צריך הרכב להפעיל עליהם גם כן כח לכיוון המרכז שגודלו ,  כאשר m היא מסת הנוסע. דרך העברתו של כח זה מהרכב לנוסעים היא דרך החיכוך ביניהם. אם אין מספיק חיכוך כדי להגיע ל-  (מה שקורה כאשר הנוסעים אינם חגורים היטב) ינוע הנוסע במסלול עם רדיוס רחב יותר מרדיוס פניית הרכב. במילים אחרות, עבור צופה שיושב ברכב, הנוסע "עף" לכיוון דופן הרכב המרוחקת יותר ממרכז הסיבוב. לעומת זאת, אם הנוסעים חגורים למקומותיהם, כח החיכוך שבינם לבין הרכב גדול דיו בכדי לסובב אותם באותו מסלול בו מסתובב האוטובוס. עכשיו נכנס לתמונה החוק השלישי של ניוטון- הרכב מפעיל על הנוסע כח לכיוון מרכז המעגל, והנוסע מפעיל על הרכב כח תגובה הפוך. בסופו של דבר מה שאנו מרגישים זה את הכח ההדדי שבינינו לבין הרכב. אם למשל, אנו יושבים בצמוד לדופן הימנית של הרכב, והוא פונה חדות שמאלה, נרגיש את הלחץ שבין כתף ימין שלנו לבין דופן הרכב.

 

:מחזוריות

כאשר עוסקים בתנועה מעגלית, כדאי ללמוד להכיר כמה מושגים המיוחדים לתנועה מחזורית, כלומר, לתנועה החוזרת על עצמה שוב ושוב-

 

זמן מחזור-

הזמן בו התנועה מספיקה לחזור למצב ההתחלתי שלה ולהתחיל עוד מחזור של תנועה. במקרה של תנועה מעגלית, זהו הזמן בו מושלם היקף שלם של המעגל. לעיתים מציינים את זמן המחזור

באות היוונית t.

תדירות-

כמה פעמים בשניה חוזרת על עצמה התנועה, כלומר, כמה פעמים בשניה התנועה "סוגרת" את כל המעגל. מציינים את התדירות ב- f או ב- n, ומודדים אותה ב'הֵרץ'.

 

חשוב לזכור את הקשר בין זמן המחזור לבין המהירות-

אם רדיוס המעגל הוא R, הרי שהיקפו הוא R×p×2 . את כל ההיקף הזה עושים בזמן מחזור t. כלומר, מהירות ההקפה (לפי זמן דרך) היא:

 

 

 

 

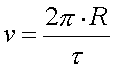
נתבונן בסרט העוסק בדוגמה נוספת של תנועה מעגלית- המטוטלת הקונית.