תלות לינארית של וקטורים
| ראינו שאפשר לייצג כל וקטור באמצעות וקטור הצירים, לדוגמה: |
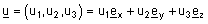
במקרה זה נאמר שהוקטור u תלוי לינארית בוקטורי הצירים.
|
הגדרה : יהיו |
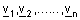 |
וקטורים. נאמר כי u תלוי לינארית בוקטורים אלו אם קיימים |
| מספרים (סקלרים) | 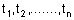 |
כך ש - | 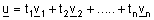 . . |
| במקרה זה נאמר גם כי u הינו צירוף לינארי של הוקטורים | 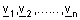 . . |
| דוגמה : האם הוקטור | 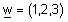 |
תלוי לינארית בוקטורים | 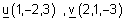 |
| פתרון : כדי להראות ש- w ת"ל (תלוי לינארית) ב- u ו v צריך להראות שקיימים סקלרים a ו b |
| כך ש- | 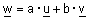 . . |
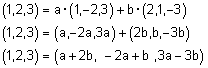
|
קבלנו 3 משוואות בשני נעלמים: |
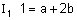 |
| נפתור אם כן 2 משוואות ונציב את הפתרונות במשוואה השלישית. | 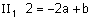 |
| אם יתקבל פסוק אמת אזי הם ת"ל אחרת הם בת"ל (בלתי תלויים לינארית) | 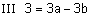 |
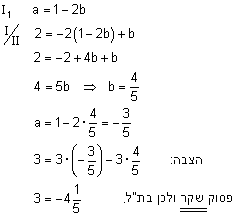
| משפט : יהיו | 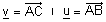 |
שני וקטורים בעלי מוצא משותף. אזי u ת"ל ב- v אם ורק אם |
| A,B,C על אותו ישר. |
| משפט : יהיו | 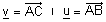 |
שני וקטורים בעלי מוצא משותף שאינם על אותו ישר |
| ויהי | 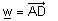 |
. נאמר כי w ת"ל ב- u ו v אם A,B,C,D נמצאים באותו מישור. |
| משפט : יהיו | 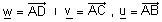 |
שלשה וקטורים בעלי מוצא משותף שאינם באותו |
| מישור. |
| ויהי | 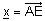 |
. נאמר כי x ת"ל ב- u , v ו w אם A,B,C,D,E נמצאים באותו מרחב. |
|
כלומר - כל וקטור במרחב,ת"ל בכל שלשה וקטורים בעלי מוצא משותף ושאינם באותו מישור. |
| דוגמה : הראה כי הנקודות | 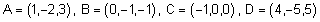 |
| נמצאות במישור אחד. |
| פתרון : לשם כך יש להראות כי ישנם 3 וקטורים כך ששניים מהם בעלי מוצא משותף ואינם על |
| ישר ,והשלישי ת"ל בהם. לכן נגדיר 3 וקטורים שראשיתם בנקודה A. |
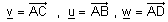
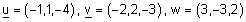
| u ו v אינם על ישר אחד כיוון שלא קיים סקלר t כך ש- u = tv . ולכן הם קובעים מישור. |
| w ת"ל ב - u ו v אם קיימים שני סקלרים s ו t כך ש- | 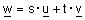 . . |
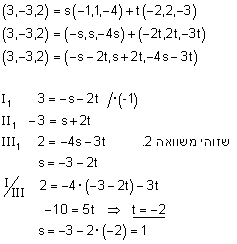
|
לכן ארבעת הנקודות נמצאות במישור אחד. w נמצא במישור הנפרש ע"י u ו v. |
| משפט : יהיו u ו | 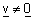 |
שני וקטורים. אזי u ת"ל ב- v אם ורק אם הוא על אותו ישר או על ישר |
| המקביל ל- v. |
| משפט : יהיו u ו | 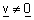 |
שני וקטורים, כאשר v נמצא במישור |  |
. u ת"ל ב- v אם ורק אם u |
| במישור |  |
או על ישר המקביל למישור. |

