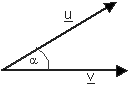
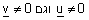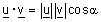זוית בין וקטורים - כל שני וקטורים (גם אם אינם יוצאים מאותה נקודת מוצא) יוצרים זוית.

                            זוית זו נמדדת ברדיאנים או במעלות.

המכפלה הסקלרית - מספר שתלוי באורכי צלעות הוקטורים (היוצאים מאותה נקודה) ובזוית

                                 שביניהם.

הגדרה : יהיו u , v שני וקטורים בעלי אותה נקודת מוצא ותהי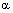

הזוית שביניהם אזי המכפלה

הסקלרית שלהם שתסומן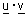

מקיימת :

(א) אם		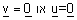אז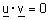
(ב) אם		אז

הערות :  (1) תזכורת :		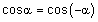ולכן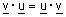
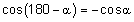		ולכן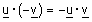

(2) כאשר הזוית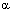

בין u ל- v ישרה (כלומר כאשר u ו v ניצבים (אורתוגונליים) זה לזה נקבל -

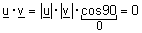
הסכם - וקטור האפס ניצב לכל וקטור.

(3) כאשר u = v נקבל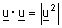

כלומר אורך הוקטור u הוא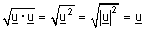

(4) אין לבלבל בין סימן הכפל בין מספרים לסימן הכפל במכפלה סקלרית בוקטורים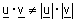

עבור u,v וקטורים שונים מוקטור האפס, אם u ו v ניצבים זה לזה אז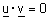

אבל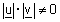

משפט : המכפלה הסקלרית מקיימת את החוקים הבאים:

(א) חוק החילוף -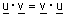
(ב)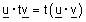
(ג) חוק הפילוג -

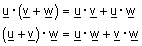כמוכן מתקיים :

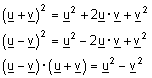
משפט : יהיו u ו v שני וקטורים שאינם על אותו ישר, ויהי w וקטור המקיים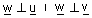

אזי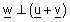

, כלומר אם ישנו וקטור שמאונך לכל אחד מהוקטורים אזי הוא גם אנך לסכומם.

ניתן להשתמש במכפלה הסקלרית, כדי לחשב (אורכים, זויות) וכדי להוכיח משפטים.