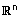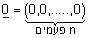| כמו במרחב הוקטורי גיאומטרי, גם במרחב | 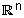 |
מתקיימות התכונות הבאות: |
| (1) סגירות בחיבור - לכל שני וקטורים מ- | 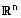 |
גם סכומם u + v הוא איבר ב - |
|
| (2) חוק הקיבוץ - יהיו u ,v ,w וקטורים ב- | 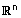 |
אזי - | 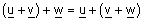 |
|
(3) איבר נייטרלי בחיבור -האיבר |
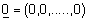 |
(n פעמים) ב- |
|
ולכל וקטור u ב | 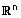 |
| מתקיים: | u + 0 = 0 + u = u . |
|
|
נקרא גם וקטור האפס.
|
| (4) איבר נגדי - לכל איבר u ב- | 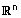 |
קיים איבר נגדי המסומן u- המקיים: |
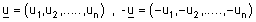
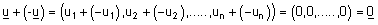
|
(5) חוק החילוף - לכל u ו v וקטורים ב- |
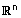 |
מתקיים : u + v = v + u. |
| (6) סגירות בכפל - לכל וקטור u ב- | 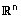 |
ומספר ממשי t מתקיים ש tu גם ב- | 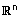 . . |
| (7) חוק הקיבוץ - לכל u ב- | 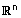 |
ולכל s , t מספרים ממשיים מתקיים: | 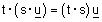 |
| (8) חוק הפילוג (לגבי סקלרים) - לכל u ב- | 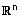 |
ולכל s,t מספרים ממשיים מתקיים: |
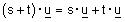
| חוק הפילוג (לגבי וקטורים) - לכל v,u ב- | 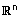 |
ולכל t מספר ממשי מתקיים: |
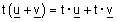
| דוגמה : יהיו | 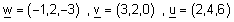 |
חשב : |
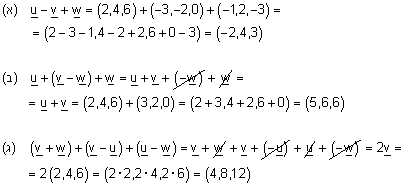


 .
.