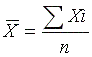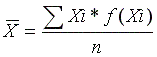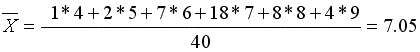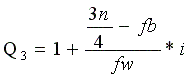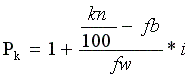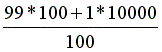|
סכום הערכים מחולק במספרם.
סימון: כאשר נתונה לנו רשימת ציונים, מחושב הממוצע בדרך הבאה:
כאשר נתונה לנו טבלת שכיחויות, נחשב את הממוצע בדרך הבאה:
ציוניהם של 40 תלמידי כיתה סוכמו בטבלת שכיחויות.
| |
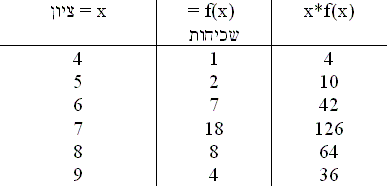 | |
|
סה"כ: 282 סה"כ: 40 | |
|
על מנת לחשב את הממוצע נסכם את המספרים בדרך הבאה ונחלק ב- n:
| |
|
| |
|
באופן דומה לחציון, ניתן לחשב גם ערכים אחרים המחלקים את הנתונים לשתי קבוצות שונות .בגודלן
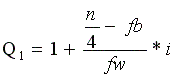
כך למשל הערך המחלק את הנתונים כך ש- %25 מהם נמוכים ממנו ו- %75 גבוהים ממנו נקרא הרבעון הראשון (התחתון), ויסומן כך: Q1.
באותו אופן נדבר על רבעון שלישי (העליון), שיסומן כך: Q3.
הרבעון השני הינו בעצם החציון.
| |
|
|
|
|
כאשר:
l - בסיס תחתון (מדומה) של הקטגוריה בה נמצא הרבעון
n - גודל המדגם
fb - השכיחות מתחת לקטגוריה בה נמצא הרבעון
fw - השכיחות בקטגוריה בה נמצא הרבעון
i - גודל המרווח
באופן כללי עבור אחוזונים שונים: (למשל עשירון עליון או תחתון) נשתמש בנוסחא:
| |
|
| |
|
כאשר:
l - בסיס תחתון (מדומה) של הקטגוריה בה נמצא האחוז
n - גודל המדגם
fb - השכיחות מתחת לקטגוריה בה נמצא האחוז
fw - השכיחות בקטגוריה בה נמצא האחוז
i - גודל המרווח | |
|
במפעל 100 עובדים, אשר 99 מהם נוסעים לצורך עבודתם כ-100 ק"מ לחודש ואילו עובד אחד נוסע כ- 10,000 ק"מ בחודש.
| |
|
ממוצע הנסיעות לעובד הינו 199 ק"מ =
ברור שממוצע זה אינו משקף כהלכה את הנתונים! לעומתו החציון (ובמקרה זה גם השכיח) ישקף את הנתונים בצורה יותר נאמנה. | |
|
 |
||
יום שבת 26 באפריל 2025
|
|
|
|||||||||||||||||||||||||||||