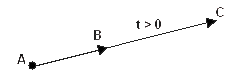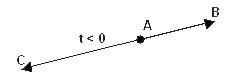כפל של וקטור במספר (סקלר) - על מנת להבין את משמעות כפל מספר בוקטור נתבונן תחילה ב-
|
נקבל שהוקטור 2u הוא בעל אותו כיוון כמו u ואורכו פי 2 מ- u.
u + u = 2u |
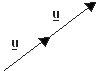 |
|
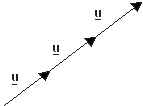
נקבל שהוקטור 3u הוא בעל אותו כיוון כמו u ואורכו פי 3 מ- u.
u + u + u = 3u
|
 |
|
נקבל שהוקטור 2u- הוא בעל כיוון מנוגד ל u ואורכו פי 2 מ-
(u) + (-u) = (-2u-) |
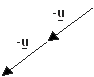 |
|
הגדרה : לכל מספר ממשי t |
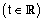 |
ולכל וקטור |  |
השונה מאפס, הוקטור | 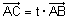 |
מקיים:
|
(א) אורכו שווה למכפלת המספר בערכו המוחלט של הוקטור |
 |
, דהיינו : | 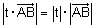 . . |
| (ב) הוקטור | 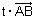 |
מקביל ל- |  . . |
|
(ג) עבור t > 0 כיוונו זהה לכיוון הוקטור
עבור t < 0 כיוונו זהה לכיוון הוקטור |
|
|
| הערה : אם t = 0 או | 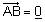 |
(או שניהם) אזי : | 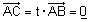 . . |
| משפט : עבור כל נקודה C על הישר AB קיימת נקודה אחת ויחידה t המקיימת | 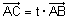 |
. |
| ולהפך, עבור כל מספר ממשי t קיימת נקודה אחת ויחידה C על הישר כך ש - | 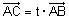 . . |