|
לעיתים קרובות צמודה לטבלת השכיחויות גם הצגה גרפית של השכיחויות. הצגה זו קלה לתפיסה, ומדגישה תכונות אופייניות שונות של הנתונים. אנו נדון בשתי הצגות חזותיות - דיאגרמת מקלות והיסטוגרמה.
דיאגרמת מקלות
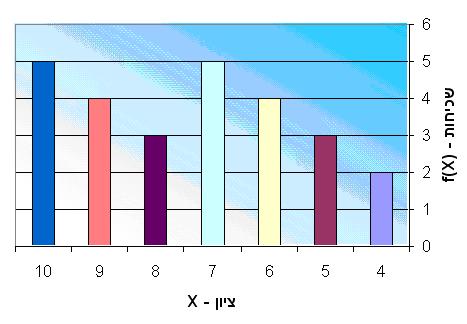
דיאגרמת מקלות היא הצגה גרפית שבה ציר x מהווה את ציר המשתנה ואילו ציר y את ציר השכיחות f(x). השימוש בדיאגרמה מסוג זה נפוץ כאשר נתונה התפלגות שכיחויות של משתנה מקרי בדיד, כלומר כאשר כל מחלקה מורכבת מערך אחד בלבד.
| |||||
|
| ||||
|
למשל ניתן לראות באופן חזותי שהציון 4 הוא בעל השכיחות הנמוכה ביותר.
היסטוגרמה
תיאור גרפי שבו ציר x מהווה את ציר המשתנה, מחלקה מיוצגת ע"י קטע על ציר x שקצותיו הן גבולות המחלקה. מעל הקטע המייצג את המחלקה בונים מלבן ששיטחו פרופורציונלי לשכיחות המחלקה כלומר, שטח המלבן, שמעל לקטע מייצג את שכיחות המחלקה.
השימוש בהיסטוגרמה נהוג במקרים שבהם התפלגות השכיחויות מקובצת במחלקות ואלו נתונות בגבולות אמיתיים. כיצד בונים היסטוגרמה?
נמחיש באמצעות הדוגמא הבאה.
| |||||
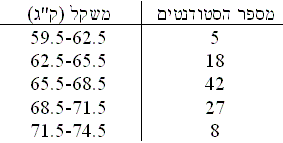
| |||||
|
א. על צירx מציינים את הגבולות האמיתיים של המחלקה כאשר מרכזיהם מתלכדים עם הערכים המרכזיים של הקבוצות ואורכן שווה לגודל של מרווחי הקבוצות. לשם הנוחות נבחר קבוצות שמרווחיהן שווים בגודלם (אצלנו הרווח שווה ל-3).
ב. שטחים פרופורציונלים לשכיחות של הקבוצות. כלומר נבנה שטח של ריבוע אחד שצלעו כאורך הרווח של המחלקות, 3, ונצייר מס' ריבועים אחד מעל השני כשכיחות שלהם. לדוגמא: לרווח השני (62.5-65.5) נצייר 6 ריבועים כאלה (6=18/3).
ג. נהוג לחבר את מרכזי הבסיסים העליונים של המלבנים בהיסטוגרמה. הקו השבור המתקבל נקרא פוליגון (מצולע).
| |||||
|
| |||||
|
| |||||
|
 |
||
יום חמישי 3 באפריל 2025
|
|
|
|||||||||||||||||||||||||||||